さて、本日は2点の緯度経度から距離を計測する方法について紹介しようと思います。平面上の単純な2点間の距離計測などは簡単にできるかと思いますが、地球は回転楕円体なため（実は地球は完全な球体というわけではありません）、その丸みを考慮した計算が必要になります。

地球の形については国土地理院さんが公開しているサイトをご参照ください。

距離計算方法

ヒュベニの公式というものがあり、こちらであれば簡易的に距離計測をすることができますので、今回はこちらを使ってみます。公式については以下をご参照ください。

ヒュベニの公式

２点間の距離計測式 D = SQRT((Ay * M)^2 + (Ax * N * cos(P))^2)

Ax：２点の経度の差
Ay：２点の緯度の差
P：２点の緯度の平均

M = Rx (1 - e＾2 )/W³：子午線曲率半径
N = Rx/W：卯酉線曲率半径
W = SQRT(1 - E＾2*sin(P)²)：子午線・卯酉線曲率半径の分母

e = SQRT((Rx² - Ry²)/Rx²)：第1離心率
Rx：長半径（赤道半径）
Ry：短半径（極半径）
E2 = e²：第2離心率

長半径（赤道半径）、短半径（極半径）という見慣れない単語がありますが、こちらに関しては Wikipediaを参照してください。そういう固定値を使うという認識でまずは大丈夫だと思います。

f:id:sanvarie:20210116195907p:plain

色々調べてみると他には以下のような計算方法があるようです。国土地理院さんが公開している計算方法は複雑すぎて私の頭では理解できないですね・・・

国土地理院方式
球面三角法
測地線航海算法

距離計測する区間

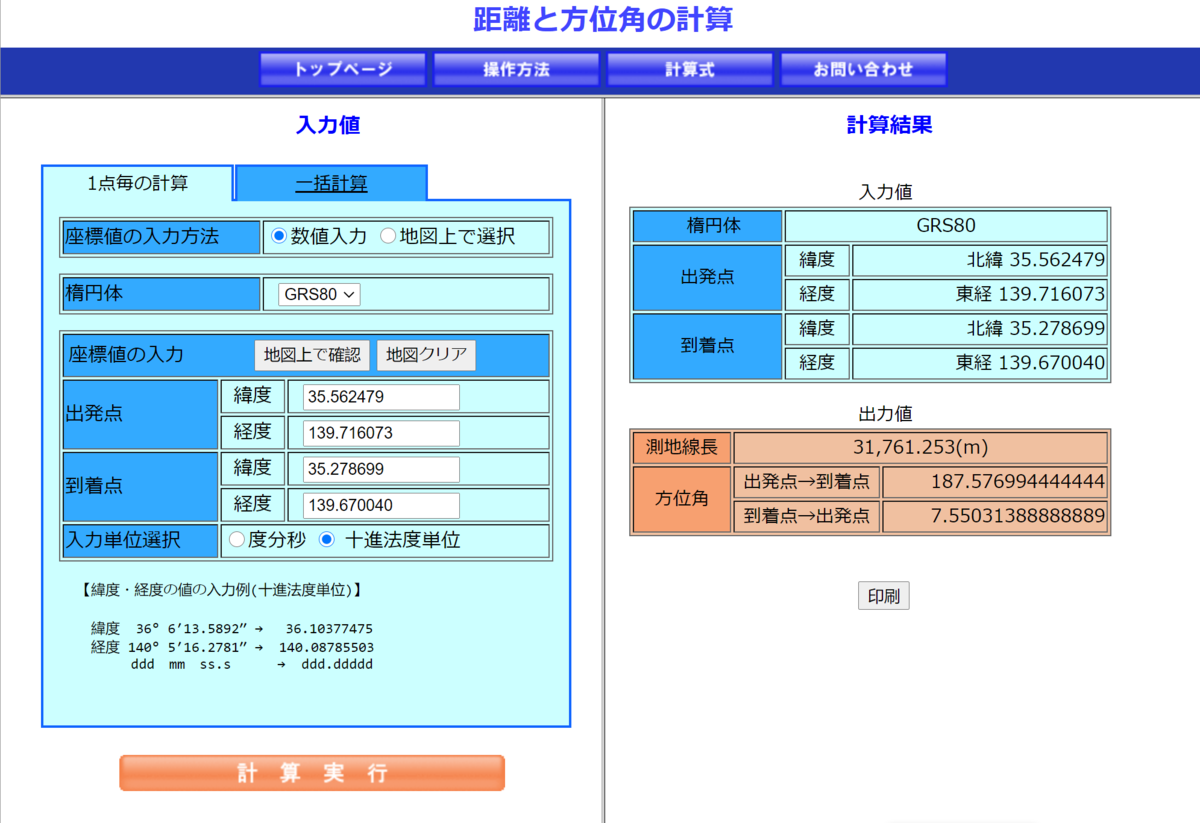
「蒲田駅」から「横須賀中央駅」の距離を計測してみようと思います。それぞれの緯度経度は以下です。

蒲田駅
- 緯度 35.562479
- 経度 139.716073

f:id:sanvarie:20210116143305p:plain

横須賀中央駅
- 緯度 35.278699
- 経度 139.670040

f:id:sanvarie:20210116143410p:plain

国土地理院さんのサイトで確認したら「31.761253km」という計測結果が出ました。今回の結果がこの数値にどれだけ近づけるかのでしょうか。楽しみです。

f:id:sanvarie:20210116151537p:plain

実行環境

Windows 10 64bit
Python 3.6.6

サンプルコード

# -*- coding: utf-8 -*-
import math

pole_radius = 6356752.314245                  # 極半径
equator_radius = 6378137.0                    # 赤道半径
latlon_kamata = (35.562479, 139.716073)       # 蒲田駅の緯度経度
latlon_yokosukachuo = (35.278699, 139.670040) # 横須賀中央駅の緯度経度

def cal_distance():

    # 緯度経度をラジアンに変換
    lat_kamata = math.radians(latlon_kamata[0])
    lon_kamata = math.radians(latlon_kamata[1])
    lat_yokosukachuo = math.radians(latlon_yokosukachuo[0])
    lon_yokosukachuo = math.radians(latlon_yokosukachuo[1])

    lat_difference = lat_kamata - lat_yokosukachuo       # 緯度差
    lon_difference = lon_kamata - lon_yokosukachuo       # 経度差
    lat_average = (lat_kamata + lat_yokosukachuo) / 2    # 平均緯度

    e2 = (math.pow(equator_radius, 2) - math.pow(pole_radius, 2)) \
            / math.pow(equator_radius, 2)  # 第一離心率^2

    w = math.sqrt(1- e2 * math.pow(math.sin(lat_average), 2))

    m = equator_radius * (1 - e2) / math.pow(w, 3) # 子午線曲率半径

    n = equator_radius / w                         # 卯酉線曲半径

    distance = math.sqrt(math.pow(m * lat_difference, 2) \
                   + math.pow(n * lon_difference * math.cos(lat_average), 2)) # 距離計測

    print(distance / 1000)

if __name__ == '__main__':
    cal_distance()

以下のような結果になりました。

f:id:sanvarie:20210116151941p:plain

「31.7612541505034km」という計測結果が出ました。国土地理院さんのサイトで計測した「31.761253km」とほぼ同じ値になりました。

さいごに

少し複雑な計算式でしたが、蒲田駅～横須賀中央駅間の距離計測に成功しました。今度は球面三角法など他の計算方法も試してみたいですね。

また、ライブラリなどを使用すればこのような計算をしなくてもいいのですが、今回のエントリーを書くにあたって色々調査をする中で勉強になることがたくさんありました。私は GIS 歴はけっこう長いのですが地理的な知識に関してはあまりなく、GIS に携わるものとして地理の基礎的な勉強をもっとしなければいけないなと実感しました。本日は以上です。

参考サイト

https://www.trail-note.net/tech/calc_distance/
http://hp.vector.co.jp/authors/VA002244/yacht/geo.htm

GIS奮闘記

元GISエンジニアの技術紹介ブログ。主にPythonを使用。

Python で2点の緯度経度から距離を計測する方法